Statistics

Statistical analysis is a method used to evaluate and analyze data sets in order to make informed decisions. There are four main types of statistical analysis: descriptive, diagnostic, predictive, and prescriptive. Descriptive statistics summarize and describe the features of a data set, while diagnostic statistics help identify issues or problems within the data. Predictive statistics use data from the past to make predictions about the future, and prescriptive statistics provide recommendations for actions to take based on the data. Statistical analysis has a long history, dating back to ancient civilizations that used data to make decisions about agriculture and trade. Today, statistical analysis is used in a wide range of fields, including business, economics, and the social and natural sciences. 

The statistical analysis that we are conducting focuses only on US listed large cap stocks as the studies population. This includes only US listed stocks with a market capitalization over ten billion dollars. We are concerned with the equal weighted representation of these stocks as opposed to the more common cap weighted representation of indexes.

The central limit theorem is a fundamental statistical concept that states that the distribution of the mean of a large number of independent and identically distributed random variables is approximately normal, regardless of the distribution of the individual variables. This means that, as the sample size increases, the distribution of the sample mean becomes more and more normal, with a mean equal to the population mean and a standard deviation inversely proportional to the sample size. The central limit theorem has wide-ranging applications in statistical inference and has been used to establish the validity of many statistical tests and procedures. It was first stated by French mathematician Abraham de Moivre in the early 18th century, and has since been refined and proven by many other mathematicians and statisticians. 

Accepting the tenets of the central limit theorem we can conclude that random samples of sufficient size will result in returns normally distributed around the equal weighted return of the population of large cap stocks as a whole and the return of this population is an acceptable return for our portfolio. As a reminder 68% of all samples are within one standard deviation of the population mean, 95% will be within two standard deviations and 99.7% of all samples will be within three standard deviations of the mean.

Random sampling is a method of selecting a representative sample from a larger population. It is important in statistical analysis because it helps to ensure that the sample accurately reflects the characteristics of the population. This is important because statistical inferences, such as estimating the mean or testing a hypothesis, are only valid if the sample is representative of the population. To obtain a truly random sample, each member of the population must have an equal chance of being selected. This helps to eliminate bias and ensures that the sample is representative of the population as a whole. Without random sampling, the results of statistical analysis may be misleading and inaccurate. 

Random sample selection is a logical process which can use any of the four traditional methods but generally the principle is that any stock in this population universe can end up in any random group. Using the research from Nassim Talebs ‘Fooled by Randomness’ we believe that the ranked samples from the 120 factors we track are as random as using the traditional methods. It could be argued that these ranked factor groups render CLM not applicable. In this matter only our research will be able to provide the proof and we will provide the distribution of returns for these ninety six portfolios at the end of each month in the Risk Analysis section.

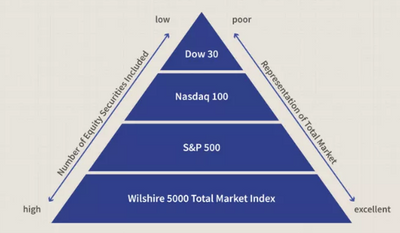
Stock indexes are a way to measure the performance of a group of stocks. They are created by taking a representative sample of stocks from a particular market or sector, and calculating the value of the index based on the price of those stocks. This value is then used as a benchmark to compare the performance of individual stocks or portfolios. Stock indexes are useful for investment management and strategy because they provide a way to track and analyze the overall performance of the market or a specific sector. They can also be used as a way to diversify a portfolio and reduce risk by investing in a broad range of stocks rather than just a few individual ones.

The stock market index that we have chosen as the benchmark for our fund is the S&P 500 index as represented by the SPDR S&P 500 ETF Trust ticker (SPY). The Invesco S&P 500 Equal Weight ETF Trust ticker (RSP) would also be a good benchmark as it is more representative of a larger number of stocks. As these indexes actually track quite similarly over time varying only as preference for the largest mega cap stocks dominate the market we will stick with the much larger SPY as it is involved in many more academic studies which are critical to a statistical strategy.

The S&P 500 index is a benchmark for the stock market, representing the performance of 500 large companies listed on the New York Stock Exchange and NASDAQ. Each month, the index is calculated based on the market capitalization of these companies. Historically, the S&P 500 has shown fluctuations in monthly performance, with some months experiencing gains while others see losses. These fluctuations can be influenced by various factors such as economic conditions, company earnings, and political events. It is important for investors to track the monthly performance of the S&P 500 as it can provide insight into the overall health of the stock market.

A major assumption that we also make is that the performance of our population of US listed stocks and random portfolio samples will follow the historical norms of the S&P 500 from 1950 through 2020 and beyond. The most important being that 6 out of 10 months will positive and 4 out of 10 negative. The average of positive months will be +3% and negative months -3% with the average of min months being -10% and max months +10% with a standard deviation of 4% and standard error of .5%.

The S&P 500 index, a benchmark for the U.S. stock market, has a history of both winning and losing streaks. A winning streak is defined as a string of positive monthly returns, while a losing streak is defined as a string of negative monthly returns. Historically, the S&P 500 has had both long and short winning and losing streaks. While the longest winning streak on record was 10 months in the 1990s, the longest losing streak was only 6 months during the financial crisis of 2008-2009. There are patterns in these monthly returns, such as a tendency for the market to experience a losing streak after a prolonged period of gains. Additionally, losing streaks tend to happen during economic downturns or recession.

Finally the historical monthly winning and losing streaks from 1950 through 2020 will continue going forward and we accept the probability that we will also undergo the frequency of these up and down months. The summary of these streaks are as follows; Winning streaks ranged from 1 through 10 straight months with the mean combined return ranging from 4 to 33%, min returns of 0 to 26%, max returns of 16 to 44%, standard deviation of 3 to 10% and standard error of .4 to 6%. Losing streaks ranged from 1 through 6 straight months with the mean combined return ranging from -3 to -12%, min returns of -11 to -15%, max returns of 0 to -9%, standard deviation of 2.1 to 3.3% and standard error of .2 to 1.9%.